On sine and cosine
Relating the geometric intuitions of sine and cosine, to their formal expressions in terms of Taylor series.
→ [preprint] ←
In the context of the picture below, the reader probably learned in high-school to define \(\cos \theta\) and \(\sin \theta\) as the \(x\) and \(y\) coordinates of point \(P\).
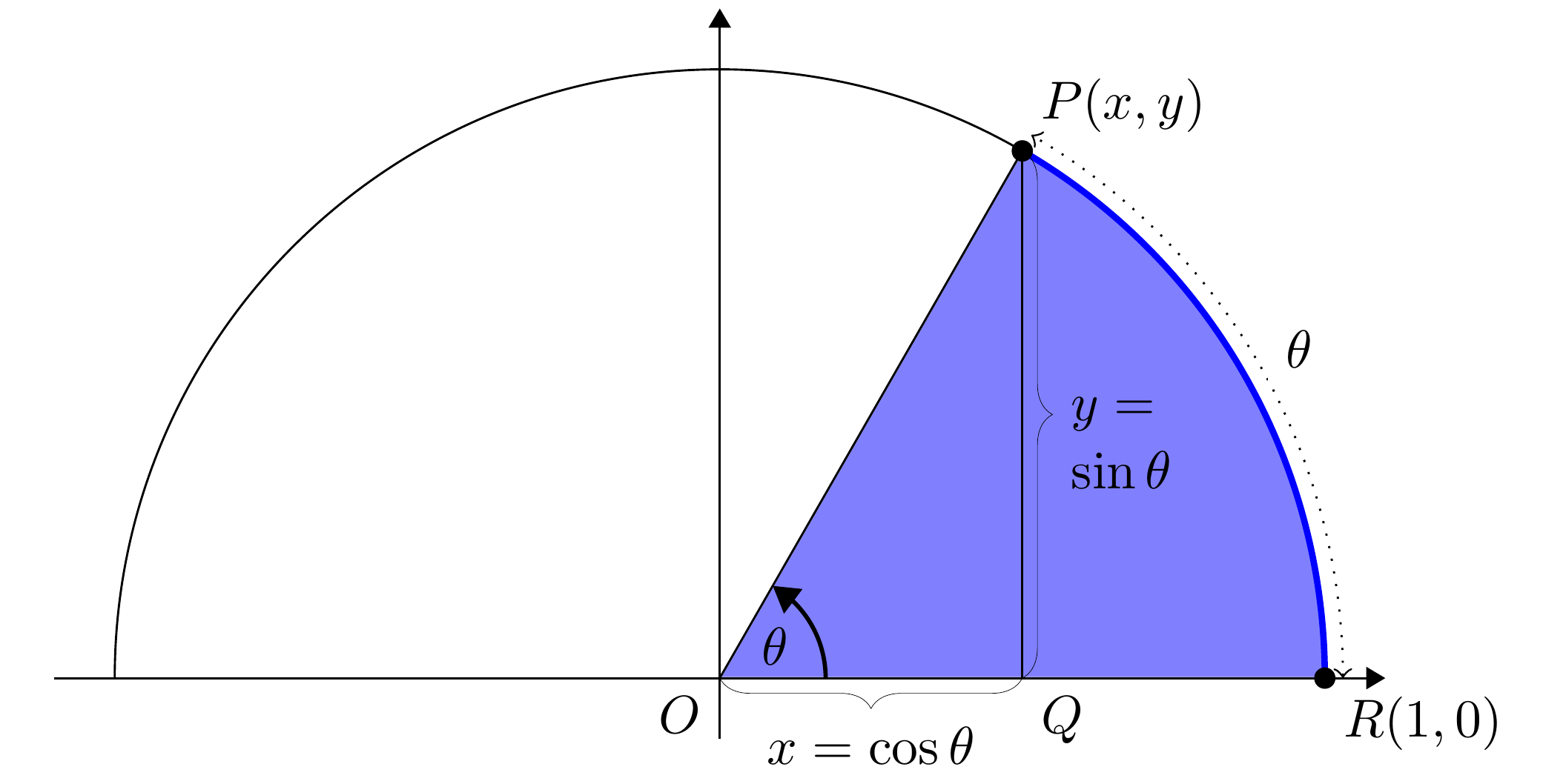
The problem is that these non-rigorous definitions, are completely detached from what one learns later (usually in undergraduate analysis), namely to define cosine and sine in terms of their Taylor series:
\[ \cos x = \sum_{n = 0}^{+\infty} \left( (-1)^n \frac{x^{2n}}{(2n)!}\right) \quad \textrm{ and } \quad \sin x = \sum_{n = 0}^{+\infty} \left((-1)^n \frac{x^{2n + 1}}{(2n + 1)!} \right) \]
This paper bridges that gap, by defining \(\cos \theta\) in terms of the area of the corresponding sector (in purple in the image), and from there deriving everything else: the definition of \(\sin \theta\), the Taylor expansions of both, and some usual properties of these functions (e.g. the sine and cosine of sums, etc.).
August 28, 2023. Got feedback? See the contact page.
Preprint update, February 21, 2024. Big overhaul of the paper.
Function \(A\), the basis for defining cosine formally, is now first proved to be a bijection, which simplifies explaining why it is suited to be used to define cosine.
Extending sine and cosine from \([0, 2\pi]\) to all of \(\mathbb{R}\) is done in a way that no longer overlaps at \(2\pi\).
This in turn aids in explicitly proving that the derivation rules for both functions, in \(]0, 2\pi[\), also apply to \(\mathbb{R} \setminus {\pi}\)—which is now done explicitly.
Added the graphs of sine and cosine, and computed their values in some frequently used points.
Added an appendix about triangles, and therein computed their values for some more points.
Added an appendix about generic properties of periodic functions.
Preprint update, December 14, 2023. Updated the Introduction, to reflect that discussing and defining \(\pi\) is only done in Section 5.
Preprint update, December 11, 2023. The extension of sine cosine from \([0, \pi]\) to \(\mathbb{R}\) is now done first, in one go. And only after that is taken care of, is continuity of both functions proved, for all of \(\mathbb{R}\). In this manner it becomes simpler to follow the reasoning.
Preprint update, December 10, 2023. Explicitly proved the continuity of sine and cosine, both going from \([0, \pi]\) to \([\pi, 2\pi]\), and then from \([0, 2\pi]\) to \(\mathbb{R}\).
Preprint update, December 9, 2023. Corrected a few typos, and clarified the derivation of sine and cosine’s Taylor expansions.
Preprint update, October 20, 2023. Clarified the idea underlying the definition of cosine.
Preprint update, September 2, 2023. At the end of the conclusion, \(\pi\) was being defined as \(\int_{-1}^{1} \sqrt{1 - t^2}dt\), which is wrong. The correct definition of \(\pi\) is \(2\int_{-1}^{1} \sqrt{1 - t^2}dt\). This has now been corrected.